Research
Analog Computation
Many powerful biological and man-made systems contain inherently analog processing elements. Until recently there has been very little theoretical work on models of this type and many basic questions remain unresolved. We are interested in describing input-output systems governed by ordinary differential equations whose behavior robustly executes arithmetic or logical operations. We have had success in designing continuous-time dynamical systems which perform discrete operations, such as sorting numbers and data clustering, and are interested in exploring the use of flows for performing a wide range of computation. [more]

Choreography of Dynamical Systems
We have developed an experimental test bed consisting of a double circular pendulum with a radio link to transmit position data from the two of the three shaft encoders. This eliminates wires and the friction effects that go along with them. We refer to this work as "choreography" but acrobatics would have been just as appropriate. The idea is to be able to give a linguistic input to the machine and have it execute the kind of swing up, rotate, balance, etc. sequences that one might expect from an Olympian on the parallel bars. Along the way we have learned something about problems involved in enlarging the domain of stability of nonlinear systems. [more]
Control of Quantum Systems
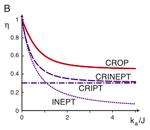
The control of quantum systems has many applications, ranging from coherent spectroscopy to quantum information processing. In most applications, the system of interest is not isolated but interacts with its environment. This leads to the phenomenon of relaxation, which in practice results in signal loss and ultimately limits the range of applications. The goal of our research is the manipulation of quantum systems in a manner that minimizes relaxation losses. Specifically, for each system we want to calculate the theoretical upper limit for the coherence transfer efficiency in the presence of relaxation and to develop optimal controls (pulse sequences) that achieve this limit experimentally.[more]
Pattern Generation
Many important engineering systems accomplish their purpose using cyclic processes whose characteristics are under feedback control. Examples involving thermodynamic cycles and electromechanical energy conversion processes are particularly noteworthy. Likewise, cyclic processes are widely found in nature and the idea of a pattern generation is widely used to rationalize mechanisms used for orchestrating movements such as those involved in locomotion and respiration. Here we develop a linkage between the use of cyclic processes and the control of nonholonomic systems, emphasizing the stable regulation of such processes. One goal is to bring out the characteristic phenomena that distinguish the regulation of such strongly nonlinear systems from more commonly studied types of feedback regulators. [more]

Robotic Manipulation
We have a six degree-of-freedom robotic manipulator known as the HRL Manipulator or the "fingers" for short. It is equipped with two deformable "fingertips" consisting of latex membranes filled with silicone. We reconstruct the shape of these membranes using computer vision and a set of assumptions in order to gain information about the shape of the fingertip. This apparatus is used as a testbed for work in robotic manipulation, particularly aspects involving tactile sensing, motion description and hybrid control. [more]
System Identification
Consider a simple linear stochastic system of the form dx = Ax dt + B dw with the state and observation noise terms dw and du being independent Wiener processes. We consider the (A,B,C) triple as unknown, and the goal of this research program is to identify (A,B,C) given the observations dy(t). This may be framed as a nonlinear filtering problem, and generally such filtering problems require an infinite number of sufficient statistics. However, the assumption that the unknown variables come from a finite set leads to a finite set of sufficient statistics. [more]
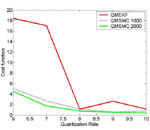
Systems with Limited Communication
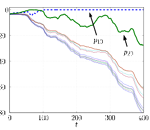
Information theoretical issues are traditionally decoupled from consideration of decision and control problems. The decoupling is achieved by ignoring the capacity constraints on communication channels connecting different components of a system. Decoupling information theoretical issues from the decision and control problems in a system greatly simplifies the analysis and generally works well for classical applications. Advances in communication, computation and networks greatly expanded the range and complexity of a control system. Many newly emerged control systems are distributed, asynchronous and networked. These systems pose challenges to the traditional assumption which ignores the communication constraints on channels among different components of a system. Integrating communication constraints into estimation and control of a system becomes an inevitable task on our way to achieve deeper understanding of distributed, asynchronous and networked control systems. [more]
