Analog Computation

Smooth Sorting

Sorting numbers seems to be an intrinsically "discrete" task. By this we mean that all intuitive algorithms to perform sorting involve a set of indivisible steps such as swapping the position of two values. Surprisingly, sorting can also be achieved in a smooth way. The following set of differential equations allows a set of unsorted numbers to flow toward the sorted state in a continuous way.

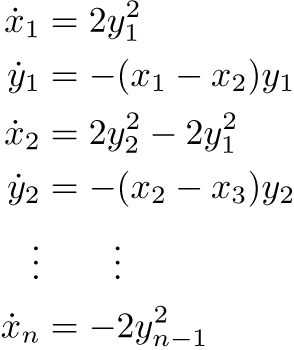
If one initializes the x variables with the numbers to be sorted and initializes the y variables with some small non-zero values, then the x variables will flow from their initially unsorted state to a sorted state. This system is also known as the nonperiodic finite Toda lattice.

A more general form is given by

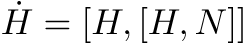
This flow has been studied extensively by Brockett et al and has been shown to be able to emulate any finite automaton in a very elegant way.

Data Clustering Flow

More recently, we used this flow to perform data clustering. In this scenario,numbers (represented also by the initial condition of the flow), will form clusters, whose value is exactly the average of its component, the clusters are formed according to the proximity of the data.

Data Representation

Our current research in analog computation focuses on answering fundamental theoretical questions. One main thrust is exploring ways in which data can be represented both robustly and generically in a continuous system. The representation of data could be designed to have other desired properties as well. For instance, one may wish to represent data such that minimal energy is used for certain computations.

Redundancy

We are also interested in understanding how redundancy could be used in an analog setting. Nature makes use of redundancy to avoid single points of failure and provide error correction in systems where noise is inevitable and fault tolerance is crucial. Redundancy could arise in either the data, or the system, or a combination of the two. For data, we can define redundancy as a triplet consisting of two sets A and B along with a surjective map , f, from A to B, such that the cardinality of A is larger than that of B. Here the set A represents our "raw" data, while B represents the "meaning" of the data. One interesting approach for representing integers in a redundant way is to consider A to be the set of all closed paths in the punctured plane and B to be the set of homotopy classes of these paths. The map f sends each curve to its corresponding homotopy class. Redundancy is obvious in this case, since A is uncountable while B is countable. If we consider the punctured plane to be phase space for a single variable, our framework has assigned many different pulses to a single integer.

Publications

Roger Brockett, "A Rational Flow for the Toda Lattice Equations," in Operators, Systems, and Linear Algebra (U. Helmke et al. eds.), B.G. Teubner, Stuggart, 1997.